Magic Circles

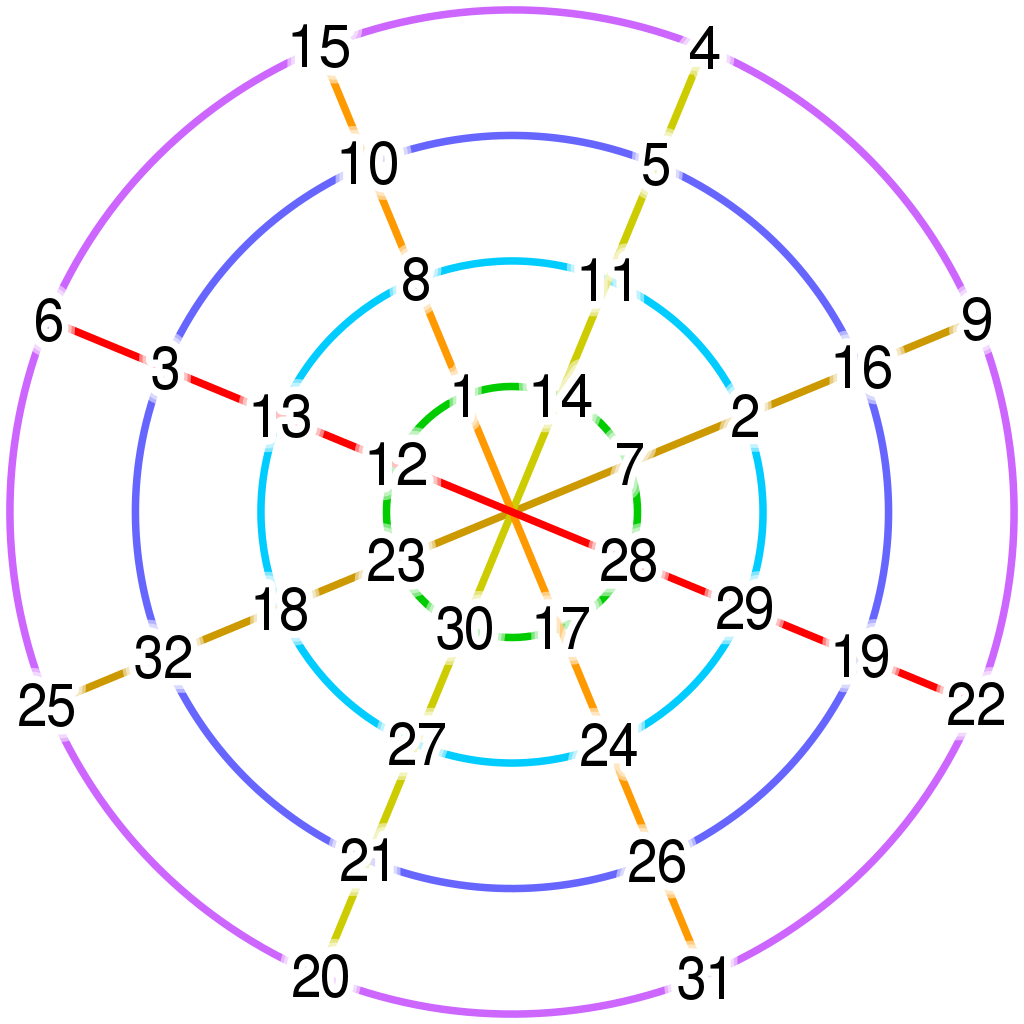
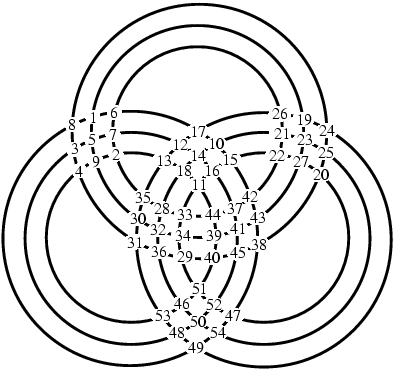
There are different types of magic circles. One of them is when ‘n’ amount of circles are intersecting each other and the numbers are located on the intersection points of these circles with eachother (on the right). If the sum of all intersections on one circle is the same for every circle, then it can be called a magic circle. To make it more clear, the numbers that are added up for every circle are the ones that all lay on intersection points with that same circle (so if you have three intersecting circles you would have to equate the sum of numbers for each circle). Magic circles to the order of 3 have a magic constant of 14 and order 4 magic circles, 39. Another type of magic circle is when the numbers 1,2,...n are arranged in a ring shape (on the left). Each ring will have the same amount of numbers, however, the outer rings will have their numbers spread out more as they are bigger. Each number is connected by their respective horizontal and vertical lines (radial lines), creating a web shape when every number is connected. The number placed in the center of all the circles is ignored and will not be included with the magic constant. Both the numbers on the rings and the numbers along the diameter of the circle, will sum up to the circle's magic constant (still ignoring the central number). There are always 2n more numbers on the rings than there are rings, so if there are four different rings subsequently, there will be eight numbers on each ring.