Magic Hexagon

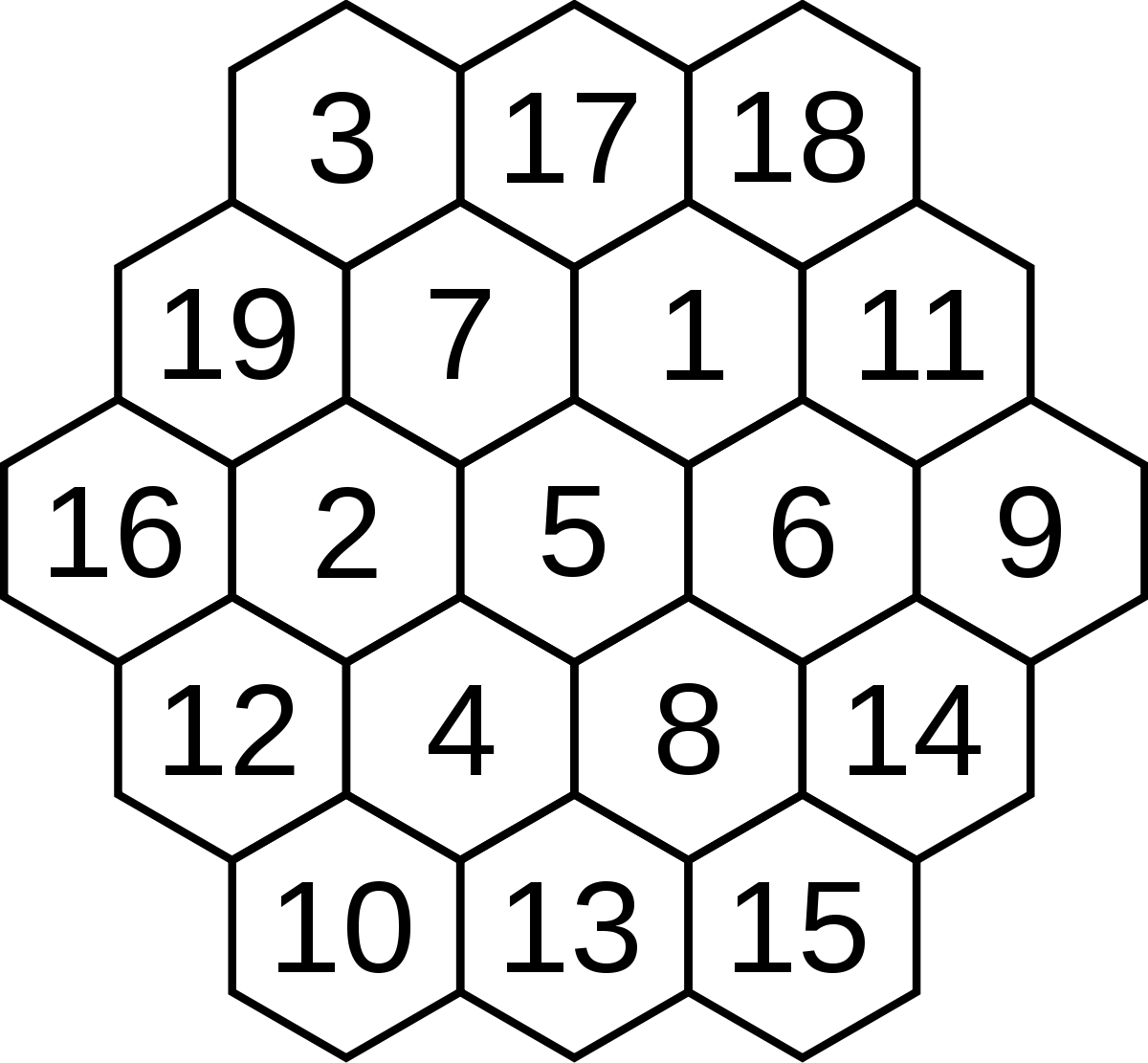
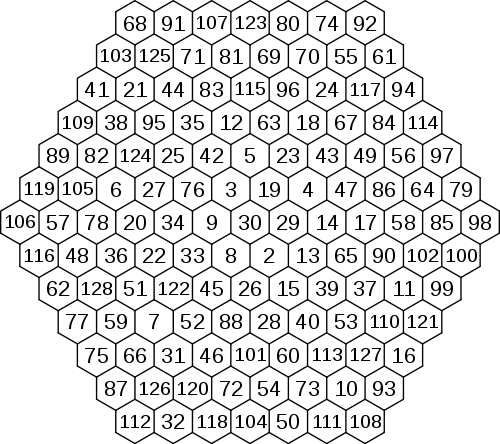
A magic hexagon exists when a set with the n th hex numbers (the amount of numbers for each order in a magic hexagon) equal to the same magic constant for each line of length n+k with k being numbers 0, 1 ,2…; The magic constant of a magic hexagon follows the formula (9($$n^4$$-2$$n^3$$+2$$n^2$$-n)-2)/(2(2n-1)). This formula was derived by Charles Watson Trigg in 1964, however the solution was discovered by many people independently, which were Ernst von Haselberg (1887), William Radcliffe (1895), Martin Kühl (1940), Clifford Adams (1910-1957) and Tom Vickers (1958). Only magic hexagons of order 1 and 3 are magic for consecutive integers, all other magic hexagons only exist with non-consecutive integers.