Bimagic Squares

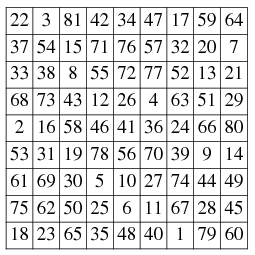
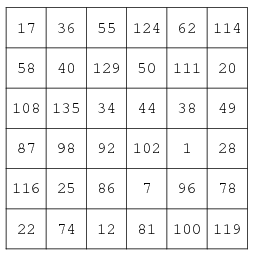
A bimagic or doubly magic square is a 2-multimagic square. This is created when in a magic square (doesn’t have to use consecutive numbers, however, with consecutive numbers the bimagic square becomes more perfect), each number is replaced by its square (1 = 1, 2 = 4, 3 = 9, etc). Georges Pfefferman was the first to discover this magic square for order 8 in 1891. Édouard Lucas was the first to prove that a 3x3 magic could not be bimagic for any set of numbers in 1891. In addition Christian Boyer and Walter Trump proved in 2002 that no bimagic squares lower than order 8 could exist. A bimagic square of order 8 has a magic constant of 260 and when squared 11180. In 2006 Jaroslaw Wroblewski found the first bimagic square of order 6, this bimagic square, however, does not have consecutive integers.